2.5.5. Berekeningsproces
[Regeling vervallen per 01-01-2024]
Voor een puntbron S van richtingsafhankelijk geluidsvermogen LW,0,dir en voor een specifieke frequentieband wordt het equivalente constante geluidsniveau
op het waarneempunt R in de gegeven atmosferische omstandigheden volgens de onderstaande
vergelijkingen verkregen.
Geluidsniveau in gunstige omstandigheden (LF) voor een pad (S,R)
|
LF = LW,0,dir– AF
|
(2.5.5)
|
De term AF geeft de totale demping weer langs het voortplantingspad in gunstige omstandigheden,
en wordt als volgt uitgesplitst:
|
AF = Adiv + Aatm+Aboundary,F
|
(2.5.6)
|
waarbij
Adiv de demping door geometrische divergentie is;
Aatm de demping door atmosferische absorptie is;
Aboundary,F de demping door de grens van het voortplantingsmedium in gunstige omstandigheden
is. De volgende termen kunnen erin vervat zijn:
-
•
Aground,F, de demping door de grond in gunstige omstandigheden;
-
•
Adif,F, de demping door diffractie in gunstige omstandigheden.
Voor een bepaald pad en bepaalde frequentieband zijn de volgende twee scenario's mogelijk:
-
• ofwel Aground,F wordt zonder diffractie (Adif,F = 0 dB) en Aboundary,F = Aground,F berekend;
-
• ofwel Adif,F wordt berekend. Het grondeffect wordt in aanmerking genomen in de Adif,F vergelijking zelf (Aground,F = 0 dB). Dit levert dus Aboundary,F = Adif,F op.
Geluidsniveau in homogene omstandigheden (LH) voor een pad (S,R)
De procedure is volkomen identiek aan het geval van gunstige omstandigheden in het
vorige gedeelte.
|
LH = LW,0,dir – AH
|
(2.5.7)
|
De term AH geeft de totale demping weer langs het voortplantingspad in homogene omstandigheden,
en wordt als volgt uitgesplitst:
|
AH = Adiv + Aatm + Aboundary,H
|
(2.5.8)
|
waarbij
Adiv de demping door geometrische divergentie is;
Aatm de demping door atmosferische absorptie is;
Aboundary,H de demping door de grens van het voortplantingsmedium in homogene omstandigheden
is. De volgende termen kunnen erin vervat zijn:
-
•
Aground,H, de demping door de grond in homogene omstandigheden;
-
•
Adif,H, de demping door diffractie in homogene omstandigheden.
Voor een bepaald pad en bepaalde frequentieband zijn de volgende twee scenario's mogelijk:
-
• ofwel Aground,H(Adif,H = 0 dB) wordt zonder diffractie en Aboundary,H = Aground,H berekend;
-
• ofwel Adif,H (Aground,H = 0 dB) wordt berekend. Het grondeffect wordt in de vergelijking Adif,H zelf in aanmerking genomen. Dit levert dus Aboundary,H = Adif,H op.
Statistische benadering in stedelijke gebieden voor een pad (S,R)
In stedelijke gebieden is een statistische benadering van de berekening van de geluidsvoortplanting
achter de eerste lijn gebouwen eveneens toegestaan, mits deze methode naar behoren
wordt gedocumenteerd, met inbegrip van relevante informatie over de kwaliteit van
de methode. Deze methode kan de berekening van Aboundary,H en Aboundary,F vervangen door een benadering van de totale demping voor het rechtstreekse pad en
alle reflecties. De berekening wordt op de gemiddelde dichtheid en gemiddelde hoogte
van alle gebouwen in het gebied gebaseerd.
Langdurig geluidsniveau voor een pad (S,R)
Het ‘langdurige’ geluidsniveau langs een pad, uitgaande van een bepaalde puntbron,
wordt verkregen uit de logaritmische som van de gewogen geluidsenergie in homogene
omstandigheden en de geluidsenergie in gunstige omstandigheden.
Deze geluidsniveaus worden gewogen door het gemiddelde optreedfrequentie p van gunstige omstandigheden in de richting van het pad (S,R):
NB: De gebeurteniswaarden voor p worden in fracties uitgedrukt. Dus indien de frequentie van optreden 82% is, krijgt
de vergelijking (2.5.9a) p = 0,82.
Optreedfrequentie per richting en periode
De gebeurteniswaarden voor p zijn richtingsafhankelijk en periode afhankelijk. De waarden p worden berekend met de volgende formules:
De voortplantingsrichting ξ is als volgt gedefinieerd:
Tabel 2.5.a Voorplantingsrichting
|
Hoek(ξ)
|
Van
|
Naar
|
|
0
|
Noord
|
Zuid
|
|
90
|
Oost
|
West
|
|
180
|
Zuid
|
Noord
|
|
270
|
West
|
Oost
|
Langdurig geluidsniveau op punt R voor alle paden
Het totale langdurige geluidsniveau op het waarneempunt voor een frequentieband wordt
verkregen aan de hand van de energetische optelling van bijdragen van alle N-paden,
met inbegrip van alle typen:
waarbij:
n de index van de paden tussen S en R is.
Het in aanmerking nemen van reflectie door middel van spiegelbronnen wordt hieronder
beschreven. De procentuele frequentie van gunstige omstandigheden bij reflectie van
een pad op een verticaal obstakel wordt geacht identiek te zijn aan de frequentie
van het rechtstreekse pad.
Als S’ de spiegelbron van S is, wordt het optreedfrequentie p’ van het pad (S’, R) beschouwd als gelijk te zijn aan optreedfrequentie p van het pad (Si, R).
Langdurig geluidsniveau op punt R in decibels A (dBA)
Het totale geluidsniveau in decibels A (dBA) wordt verkregen door de niveaus in elke
frequentieband op te tellen:
Waarbij i de index van de frequentieband is. AWC is de A-gewogen correctie als volgt:
|
Frequentie [Hz]
|
63
|
125
|
250
|
500
|
1.000
|
2.000
|
4.000
|
8.000
|
|
AWCf,i [dB]
|
–26,2
|
–16,1
|
–8,6
|
–3,2
|
0
|
1,2
|
1,0
|
–1,1
|
Dit niveau LAeq,LT vormt het eindresultaat, d.w.z. het A-gewogen geluidsdrukniveau over lange termijn
op het waarneempunt op een bepaald referentietijdsinterval (bijvoorbeeld dag, avond,
nacht of een kortere periode tijdens de dag, avond of nacht).
2.5.6. Berekening van geluidsvoortplanting voor weg-, spoor-, industriebronnen
[Regeling vervallen per 01-01-2024]
Geometrische divergentie
De demping door geometrische divergentie, Adiv, komt overeen met een vermindering van het geluidsniveau door de voortplantingsafstand.
Voor een puntbron in vrij veld wordt de demping in dB verkregen door:
|
Adiv = 20lg(d) + 11
|
(2.5.12)
|
waarbij d de rechtstreekse schuine afstand in 3D is tussen de bron en het waarneempunt is.
Atmosferische absorptie
De demping door atmosferische absorptie Aatm tijdens voortplanting over een afstand d wordt verkregen in dB door de vergelijking:
|
Aatm = αatm ∙ d⁄1.000
|
(2.5.13)
|
waarbij:
d de rechtstreekse 3D schuine afstand tussen de bron en het waarneempunt is;
αatm de coëfficiënt van atmosferische demping in dB/km op de nominale middenfrequentie
voor elke frequentieband is, in overeenstemming met ISO 9613-1.
De waarden van de αatm coëfficiënt worden gegeven voor een temperatuur van 15°C, een relatieve luchtvochtigheid
van 70% en een atmosferische druk van 101 325 Pa. Zij worden met de nauwkeurige middenfrequenties
van de frequentieband berekend. Deze waarden voldoen aan ISO 9613-1. Het meteorologische
gemiddelde op lange termijn wordt gebruikt indien meteorologische gegevens beschikbaar
zijn.
Tabel 2.5.b De luchtdempingscoëfficiënt lucht als functie van de octaafband
|
Octaafband
|
αatm [dB/km]
|
|
63
|
0,105
|
|
125
|
0,376
|
|
250
|
1,124
|
|
500
|
2,358
|
|
1.000
|
4,079
|
|
2.000
|
8,777
|
|
4.000
|
26,608
|
|
8.000
|
94,962
|
Grondeffect
De demping door het grondeffect is hoofdzakelijk het gevolg van de interferentie tussen
het gereflecteerde geluid en het geluid dat zich rechtstreeks van de bron naar het
waarneempunt voortplant. Het is fysiek verbonden aan de akoestische absorptie van
de grond waarboven de geluidsgolf zich voortplant. Het is echter ook sterk afhankelijk
van atmosferische omstandigheden tijdens voortplanting, omdat straalafbuiging de hoogte
van het pad boven de grond wijzigt en de effecten van de grond en het land in de buurt
van de bron meer of minder versterkt.
In het geval dat de voortplanting tussen de bron en het waarneempunt door een obstakel
in het voortplantingsvlak wordt beïnvloed, wordt het grondeffect aan de kant van de
bron en het waarneempunt afzonderlijk berekend. In dit geval verwijzen zs en zr naar de equivalente positie van de bron en/of het waarneempunt, zoals aangegeven
hieronder waar de berekening van de diffractie Adif wordt gepresenteerd.
Akoestische karakterisering van grond
De akoestische absorptie-eigenschappen van de grond houden voornamelijk verband met
zijn porositeit. Compacte grond is in het algemeen reflecterend en poreuze grond is
absorberend.
Voor operationele berekeningen wordt de akoestische absorptie van een grond weergegeven
met een dimensieloze coëfficiënt G, tussen 0 en 1. G is onafhankelijk van de frequentie. Tabel 2.5.c geeft de G-waarden voor de grond in de openlucht. Het gemiddelde van de coëfficiënt G over een pad krijgt in het algemeen waarden tussen 0 en 1.
Tabel 2.5.c G-waarden voor verschillende soorten grond
|
Beschrijving
|
Type
|
(kPa • s/m2)
|
G-waarde
|
|
Zeer zacht (sneeuw of mosachtig)
|
A
|
12,5
|
1
|
|
Zachte bosgrond (kort, dicht heideachtig of dik mos)
|
B
|
31,5
|
1
|
|
Niet-compacte, losse grond (veen, gras, losse aarde)
|
C
|
80
|
1
|
|
Normale niet-compacte grond (bosbodem, weiden)
|
D
|
200
|
1
|
|
Compact land en grind (compacte gazons, parkland)
|
E
|
500
|
0,7
|
|
Compacte dichte grond (grindweg, parkeerplaats)
|
F
|
2.000
|
0,3
|
|
Harde oppervlakken (veelal normaal asfalt, beton)
|
G
|
20.000
|
0
|
|
Zeer harde en dichte oppervlakken (dicht asfalt, beton, water)
|
H
|
200.000
|
0
|
Gpath wordt gedefinieerd als de fractie van absorberende grond die over het gehele pad
aanwezig is.
Wanneer de bron en het waarneempunt vlakbij elkaar zijn zodat dp ≤ 30(zs+ zr), is het verschil tussen de grondsoort nabij de bron en de grondsoort nabij het waarneempunt
te verwaarlozen. Daarom wordt om met deze opmerking rekening te houden de grondfactor
Gpath uiteindelijk als volgt gecorrigeerd:
waarbij GS de grondfactor van het brongebied is. GS = 0 voor wegdekken, betonplatenspoor. GS = 1 voor sporen in ballastbed. Er is geen algemeen antwoord in het geval van industriële
bronnen en fabrieken.
G kan gerelateerd worden aan de stromingsweerstand.
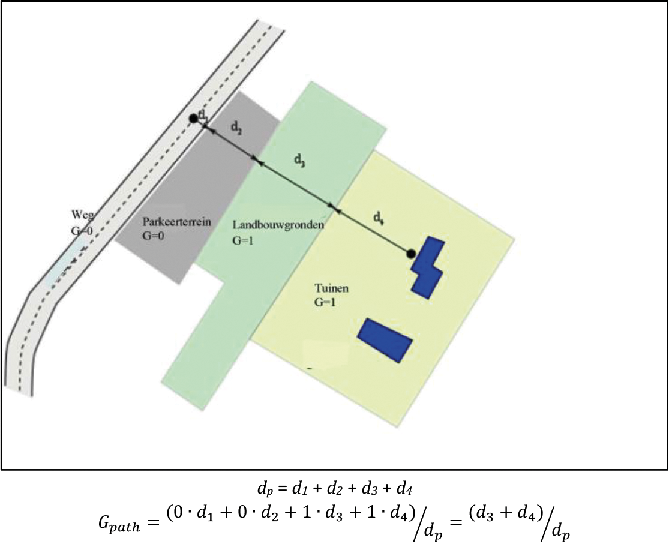
Figuur 2.5.b, Bepaling van de grondcoëfficiënt Gpath over een voortplantingspad
De afstanden dn worden bepaald door een 2D-projectie op het horizontale vlak.
De volgende twee subsecties over berekeningen in homogene en gunstige omstandigheden
introduceren de generieke
en
notaties voor de absorptie van de grond. Tabel 2.5.d geeft het verband tussen deze
notaties en de variabelen Gpath en G’path.
Berekeningen in homogene omstandigheden
De demping door het grondeffect in homogene omstandigheden wordt berekend op basis
van de volgende vergelijkingen:
indien G’path≠ 0
waarbij
fm de nominale middenfrequentie is van de frequentieband in kwestie, in Hz, c de snelheid van het geluid in de lucht is, gelijk aan 340 m/s, en Cf wordt bepaald door:
waarbij de waarden van w worden verkregen door de onderstaande vergelijking:
kan gelijk zijn aan Gpath of G’path, afhankelijk van het feit of het grondeffect met of zonder diffractie wordt berekend,
en volgens de aard van de grond onder de bron (werkelijke of afgebogen bron). Dit
wordt in de volgende subsecties vermeld en is in tabel 2.5.d samengevat.
is de ondergrens van Aground,H.
Voor een pad (Si,R) in homogene omstandigheden zonder diffractie:
= G’path
= G’path
Met diffractie, raadpleeg de sectie over diffractie voor de definities van
en
.
Indien Gpath = 0: Aground,H= -3 dB
De term
houdt rekening met het feit dat wanneer de bron en het waarneempunt ver van elkaar
liggen, het eerste reflectievlak zich niet langer op het platform maar op natuurlijke
grond bevindt.
Berekening in gunstige omstandigheden
Het grondeffect in gunstige omstandigheden wordt berekend met de vergelijking van
Aground,H, mits de volgende wijzigingen worden gemaakt:
Indien Gpath ≠ 0
-
a) In de vergelijking 2.5.15 (Aground,H) worden de hoogten zs en zr vervangen door respectievelijk zs + δzs + δzT en zr + δzr + δzT, waarbij
a0 = 2 • 10-4m-1 is het omgekeerde van de kromtestraal
-
b) De ondergrens van Aground,F (berekend met ongewijzigde hoogten) is afhankelijk van de geometrie van het pad:
Indien Gpath = 0: Aground,F = Aground,F,min
De hoogtecorrecties δzs en δzr brengen het effect van de afbuiging van de geluidstralen over. δzT verdisconteert het effect van de turbulentie.
kan ook gelijk zijn aan of Gpath of G’path, afhankelijk van het feit of het grondeffect met of zonder diffractie wordt berekend,
en volgens de aard van de grond onder de bron (werkelijke of afgebogen bron). Dit
wordt in de volgende subsecties nader bepaald.
Voor een pad (Si, R) in gunstige omstandigheden zonder diffractie:
= Gpath in vergelijking (2.5.17)
= G’path
Met diffractie, raadpleeg de volgende sectie voor de definities van
en
Diffractie
Gewoonlijk wordt de diffractie aan de bovenkant van elk obstakel op het voortplantingspad
onderzocht. Als het pad ‘hoog genoeg’ over de diffractierand loopt, kan Adif = 0 worden vastgesteld en een rechtstreeks zicht worden berekend, met name door de beoordeling
van Aground.
In de praktijk worden de volgende specificaties in aanmerking genomen in het unieke
verticale vlak dat zowel de bron als het waarneempunt bevat (een uitvouwend Chinees
kamerscherm in het geval van een traject met reflecties). De rechtstreekse straal
van de bron naar het waarneempunt is een rechte lijn onder homogene voortplantingscondities
en een gebogen lijn (boog waarvan de straal afhankelijk is van de lengte van de rechtstreekse
straal) onder gunstige voortplantingscondities.
Als de rechtstreekse straal niet is geblokkeerd, wordt de rand D gezocht die het grootste
padverschil δ oplevert (de kleinste absolute waarde, omdat deze padverschillen negatief zijn).
Diffractie wordt in aanmerking genomen als
Dit is het geval als δ groter is dan λ/4 – δ*, waarbij δ* het padverschil is dat met deze zelfde rand D is berekend, maar gerelateerd is aan
de gespiegelde bron S* berekend met het gemiddelde grondvlak aan de bronkant en aan
het gespiegelde waarneempunt R* berekend met het gemiddelde grondvlak aan de waarneemkant.
Om δ* te berekenen worden alleen de punten S*, D en R* in aanmerking genomen – andere
randen die het pad S*->D->R* blokkeren, worden verwaarloosd. Voor de bovenstaande
overwegingen wordt de golflengte λ berekend met behulp van de nominale middenfrequentie
en een geluidssnelheid van 340 m/s.
Als aan deze twee voorwaarden is voldaan, wordt de bronkant door rand D van de waarneemkant
gescheiden, worden twee afzonderlijke gemiddelde grondvlakken berekend en wordt Adifberekend zoals beschreven in de rest van dit deel. Anders wordt voor dit pad geen
demping door diffractie overwogen, wordt een gemeenschappelijk gemiddeld grondvlak
voor het pad S -> R berekend, en Aground zonder diffractie (Adif = 0 dB) berekend. Deze regel geldt zowel in homogene als in gunstige omstandigheden.
Wanneer voor een specifieke frequentieband een berekening volgens de in deze sectie
beschreven procedure wordt gemaakt, wordt Aground vastgesteld als gelijk te zijn aan 0 dB voor de berekening van de totale demping.
Het grondeffect wordt rechtstreeks in de vergelijking van de algemene diffractieberekening
in aanmerking genomen.
De hier voorgestelde vergelijkingen worden gebruikt om de diffractie op dunne schermen,
dikke schermen, gebouwen, bermen (natuurlijke of kunstmatige) en door de randen van
dijken, ingravingen en viaducten te verwerken.
Wanneer verscheidene diffractie-obstakels op een voortplantingspad worden aangetroffen,
worden ze behandeld als een meervoudige diffractie door toepassing van de procedure
die in de volgende sectie over de berekening van het padverschil wordt beschreven.
De hier gepresenteerde procedures worden voor de berekening van dempingen in zowel
homogene als gunstige omstandigheden gebruikt. Bij de berekening van het padverschil
en voor de berekening van de grondeffecten voor en na diffractie wordt rekening gehouden
met straalbuiging.
Algemene beginslen
Figuur 2.5.c illustreert de algemene methode voor berekening van de demping door diffractie.
Deze methode is gebaseerd op het opsplitsen van het voortplantingspad in twee delen:
het pad van de ‘bronkant’, gelegen tussen de bron en het diffractiepunt, en het pad
van ‘waarneemkant’, gelegen tussen het diffractiepunt en het waarneempunt.
Het volgende wordt berekend:
-
• een grondeffect, bronkant, Δground(S,O)
-
• een grondeffect, waarneemkant, Δground(O,R)
-
• en drie diffracties:
-
• tussen de bron S en het waarneempunt R: Δdif(S,R)
-
• tussen de spiegelbron S′ en R: Δdif(S′,R)
-
• tussen S en de spiegelontvanger R′: Δdif(S,R′).
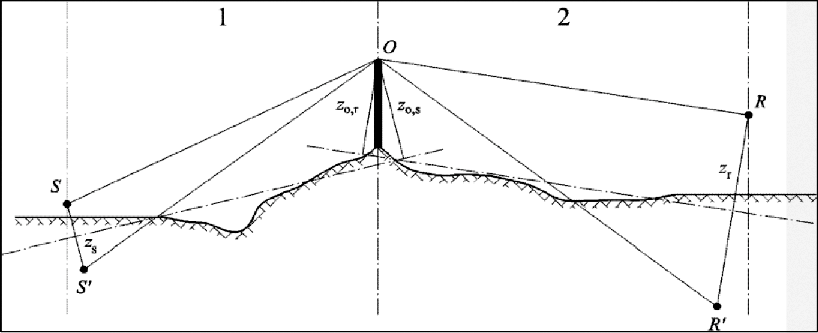
Figuur 2.5.c, Geometrie van een berekening van de demping door diffractie
-
1: Bronkant
-
2: Waarneemkant
waarbij:
S de bron is;
R het waarneempunt is;
S’ de spiegelbron is in verhouding tot het gemiddelde grondvlak aan de bronkant;
R’ de spiegelontvanger is in verhouding tot het gemiddelde grondvlak aan de waarneemkant;
O het diffractiepunt is;
zs de equivalente hoogte is van de bron S in verhouding tot het gemiddelde vlak aan de bronkant;
zo,s de equivalente hoogte is van het diffractiepunt O in verhouding tot het gemiddelde grondvlak aan de bronkant;
zr de equivalente hoogte is van het waarneempunt R in verhouding tot het gemiddelde vlak aan de waarneemkant;
zo,r de equivalente hoogte is van het diffractiepunt O in verhouding tot het gemiddelde grondvlak aan de waarneemkant.
De onregelmatigheid van de grond tussen de bron en het diffractiepunt en tussen het
diffractiepunt en het waarneempunt wordt in aanmerking genomen door middel van equivalente
hoogten berekend in verhouding tot het gemiddelde grondvlak, eerst de bronkant en
vervolgens de waarneemkant (twee gemiddelde grondvlakken), volgens de methode beschreven
in de subsectie over aanmerkelijke hoogten boven de grond (figuur 2.5.a).
Zuivere diffractie
Voor zuivere diffractie, zonder grondeffecten, wordt de demping verkregen door:
waarbij:
λ de golflengte is op de nominale middenfrequentie van de frequentieband in kwestie;
δ het padverschil is tussen het gebogen pad en het rechtstreekse pad (zie de volgende
subsectie over de berekening van het padverschil);
C’’ coëfficiënt is die wordt gebruikt om rekening te houden met meervoudige diffracties:
C’’ = 1 voor een enkele diffractie.
Voor meervoudige diffractie, indien e de totale afstand langs het pad is tussen het eerste en het laatste diffractiepunt
(gebruik bij gunstige omstandigheden gebogen stralen) en als e hoger is dan 0,3 m (anders geldt C’’ = 1), wordt deze coëfficiënt gedefinieerd door:
De waarden van ∆dif worden vastgelegd:
-
• indien ∆dif< 0: ∆dif = 0 dB
-
• indien ∆dif > 25: ∆dif = 25 dB voor een diffractie op een horizontale rand en alleen op de term ∆dif die in de berekening van Adifvoorkomt. Deze bovengrens wordt niet toegepast in de ∆dif-termen die in de berekening van ∆ground gebruikt worden, of voor een diffractie op een verticale rand (laterale diffractie)
in het geval van kartering van industrielawaai.
Berekening van het padverschil
Het padverschil δ wordt berekend in een verticaal vlak dat de bron en het waarneempunt bevat. Dit is
een benadering met betrekking tot het beginsel van Fermat. De benadering blijft hier
van toepassing (bronlijnen). Het padverschil δ wordt zoals in de volgende figuren berekend, op basis van de aangetroffen situaties.
Homogene omstandigheden
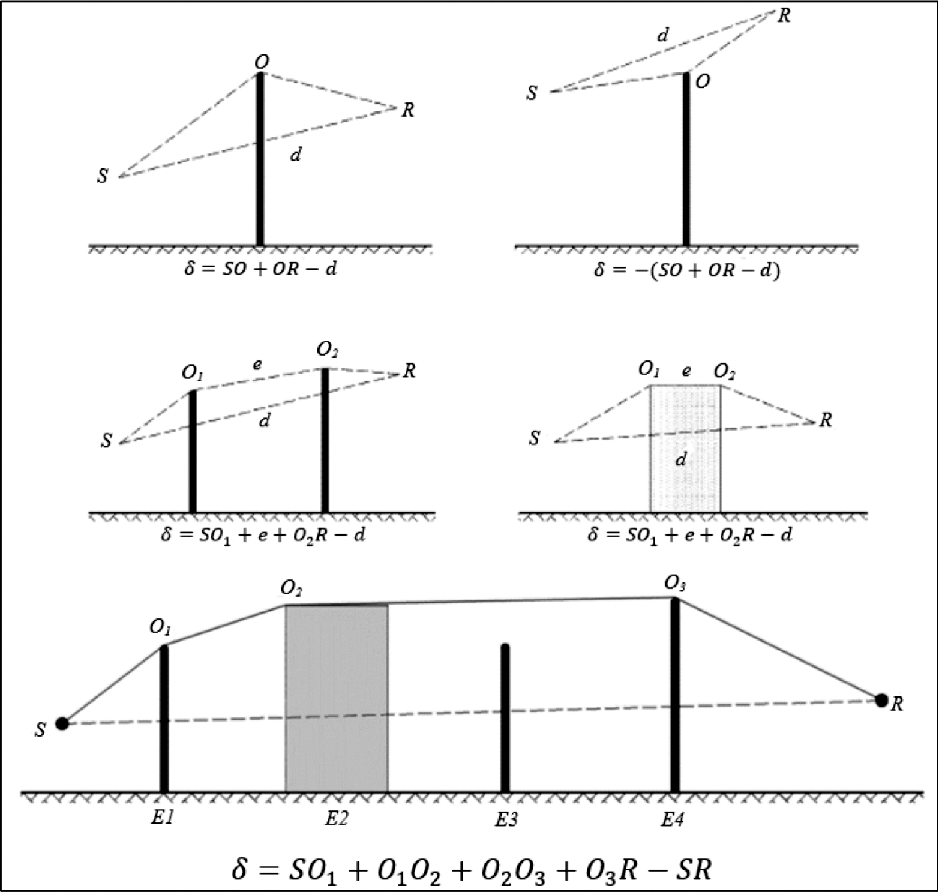
Figuur 2.5.d, Berekening van het padverschil in homogene omstandigheden. O, O1, O2 en O3 zijn de diffractiepunten
Opmerking: voor elke configuratie wordt de uitdrukking van δ gegeven.
Gunstige omstandigheden
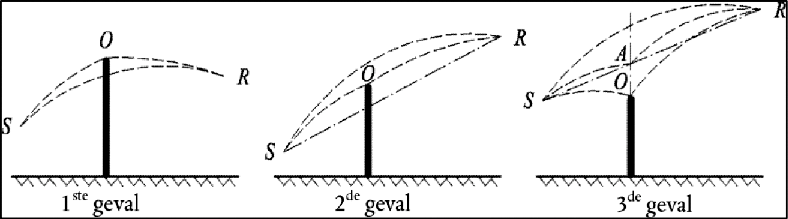
Figuur 2.5.e, Berekening van het padverschil in gunstige omstandigheden (enkele diffractie)
In gunstige omstandigheden hebben de drie gebogen geluidsstralen SO, OR en SR een identieke kromtestraal Γ, gedefinieerd door:
|
Γ = max(1.000,8d)
|
(2.5.23)
|
Waarbij d wordt gedefinieerd door de 3D-afstand tussen de bron en het waarneempunt van het
opengevouwen pad.
De lengte van de kromming van een geluidsstraal
wordt in gunstige omstandigheden aangeduid als
Deze lengte is gelijk aan:
In beginsel dienen drie scenario's in aanmerking te worden genomen in de berekening
van het padverschil in gunstige omstandigheden δF (zie figuur 2.5.e). In de praktijk volstaan twee vergelijkingen:
als de rechte geluidstraal SR door het obstakel (1e en 2e geval in figuur 2.5.e) wordt gemaskeerd:
als de rechte geluidstraal SR niet door het obstakel (3e geval in figuur 2.5.e) wordt gemaskeerd:
waarbij A het snijpunt van de rechte geluidstraal SR en het verlengde van het diffractie veroorzakende obstakel is.
Voor de meervoudige diffracties in gunstige omstandigheden:
-
• bepaal het convexe omhulsel gedefinieerd door de verschillende mogelijke diffractieranden;
-
• elimineer de diffractieranden die zich niet op de grens van het convexe omhulsel bevinden;
-
• bereken δF op basis van de lengten van de gebogen geluidsstraal door het gebogen pad in net
zo veel gebogen segmenten te verdelen als er nodig zijn (zie figuur 2.5.f)
Onder gunstige omstandigheden bestaat het voortplantingspad in het verticale voortplantingsvlak
altijd uit segmenten van een cirkel waarvan de straal wordt verkregen door de 3D-afstand
tussen de bron en het waarneempunt, d.w.z. alle segmenten van een voortplantingspad
hebben dezelfde kromtestraal. Als de directe-boogverbinding tussen de bron en het
waarneempunt geblokkeerd is, wordt het voortplantingspad gedefinieerd als de kortste
convexe combinatie van bogen die alle obstakels omhult. Convex betekent in dit verband
dat op elk diffractiepunt het uitgaande straalsegment naar beneden wordt afgebogen
ten opzichte van het inkomende straalsegment.
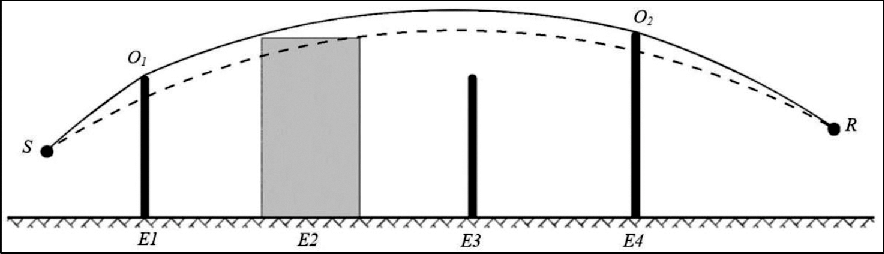
Figuur 2.5.f, Voorbeeld van berekening van het padverschil in gunstige omstandigheden,
in het geval van meervoudige diffracties
In het scenario dat in figuur 2.5.f wordt afgebeeld is het padverschil:
Berekening van de demping Adif
De demping door diffractie, waarbij de grondeffecten aan de bronkant en waarneemkant
in aanmerking worden genomen, wordt berekend op basis van de volgende algemene vergelijkingen:
|
Adif = ∆dif(S.R) + ∆ground (S,O) + ∆ground(On,R)
|
(2.5.29)
|
waarbij:
-
•
∆dif(S,R) de demping is door de diffractie tussen de bron S en het waarneempunt R,
-
•
∆ground(S,O) de demping is door het grondeffect aan de bronkant, gewogen door de diffractie aan
de bronkant. Daarbij wordt er van uitgegaan dat O = O1 in het geval van meervoudige diffracties zoals in figuur 2.5.f,
-
•
∆ground(On,R) de demping is door het grondeffect aan de waarneemkant, gewogen door de diffractie
aan de waarneemkant (zie de volgende subsectie over de berekening van de term ∆ground(On,R)).
Berekening van de term ∆ground(S,O)
waarbij:
-
•
Aground(S,O) de demping is door het grondeffect tussen de bron S en het diffractiepunt O. Deze
term wordt berekend zoals aangegeven in de vorige subsectie over berekeningen in homogene
omstandigheden en in de vorige subsectie over berekening in gunstige omstandigheden,
met de volgende hypothesen:
-
•
zr = zo,s,
-
•
Gpath tussen S en O wordt berekend,
-
• In homogene omstandigheden:
= G'path in vergelijking (2.5.17),
= G'path in vergelijking (2.5.18),
-
• In gunstige omstandigheden:
= Gpath in vergelijking (2.5.17),
= G'path in vergelijking (2.5.20),
-
•
∆dif(S’,R) is de demping door de diffractie tussen de spiegelbron S′ en R, berekend als in de
vorige subsectie over zuivere diffractie,
-
•
∆dif(S,R) is de demping door de diffractie tussen S en R, berekend als in de vorige subsectie
over zuivere diffractie.
In het bijzondere geval dat de bron onder het gemiddelde grondvlak ligt:
∆dif(S’,R) = ∆dif(S,R) en ∆ground(S,O)=Aground(S,O).
Berekening van de term ∆ground(O,R)
waarbij:
-
•
Aground(O,R) de demping is door het grondeffect tussen het diffractiepunt O en het waarneempunt
R. Deze term wordt berekend zoals aangegeven in de vorige subsectie over berekening
in homogene omstandigheden en in de vorige subsectie over berekening in gunstige omstandigheden,
met de volgende hypothesen:
-
•
zs =
zo,r,
-
•
Gpath wordt berekend tussen O en R,
De correctie G’path hoeft hier niet in aanmerking te worden genomen omdat de bron in kwestie het diffractiepunt
is. Daarom wordt Gpath wel in de berekening van grondeffecten gebruikt, inclusief voor de ondergrensterm
van de vergelijking die dan -3(1 – Gpath) wordt.
-
– In homogene omstandigheden:
in vergelijking (2.5.17),
in vergelijking (2.5.18),
-
– In gunstige omstandigheden:
in vergelijking (2.5.17),
in vergelijking (2.5.20),
-
−
∆dif(S,R’) is de demping door de diffractie tussen S en de spiegelontvanger R’, berekend als
in de vorige subsectie over zuivere diffractie;
-
−
∆dif(S,R) is de demping door de diffractie tussen S en R, berekend als in de vorige subsectie
over zuivere diffractie.
In het bijzondere geval dat het waarneempunt onder het gemiddelde grondvlak ligt:
∆dif(S,R’) = ∆dif(S,R) en ∆ground(O,R)= Aground(O,R).
Scenario's met verticale rand
Vergelijking (2.5.21) kan worden gebruikt voor de berekening van de diffracties op
verticale randen (laterale diffracties) in het geval van industrielawaai. In dit geval
wordt Adif= ∆dif(S,R) weggenomen en blijft de term Aground behouden. Bovendien worden Aatm en Aground berekend op basis van de totale lengte van het voortplantingspad. Adiv wordt nog steeds berekend vanaf de rechtstreekse afstand d. De vergelijkingen (2.5.8) en (2.5.6) worden respectievelijk:
Laterale diffractie wordt alleen in aanmerking genomen in gevallen waarin aan de volgende
voorwaarden wordt voldaan:
-
• De bron is een echte puntbron – niet geproduceerd door segmentatie van een uitgebreide
bron zoals een bronlijn of diffuse bron.
-
• De bron is geen gespiegelde bron die is geconstrueerd om een reflectie te berekenen.
-
• De rechtstreekse straal tussen de bron en het waarneempunt ligt volledig boven het
terreinprofiel.
-
• In het verticale vlak met S en R is het padverschil δ groter dan 0, d.w.z. de rechtstreekse straal wordt geblokkeerd. Daarom kan in sommige
situaties laterale diffractie in aanmerking worden genomen onder homogene voortplantingscondities,
maar niet onder gunstige voortplantingscondities.
Als aan al deze voorwaarden is voldaan, wordt naast het gebogen voortplantingspad
in het verticale vlak met de bron en het waarneempunt rekening gehouden met maximaal
twee lateraal gebogen voortplantingspaden. Het laterale vlak is gedefinieerd als het
vlak dat loodrecht staat op het verticale vlak en ook de bron en het waarneempunt
bevat. De snijvlakken met dit laterale vlak zijn opgebouwd uit alle obstakels die
door de rechtstreekse straal van de bron naar het waarneempunt worden doorsneden.
In het laterale vlak bepaalt de kortste convexe verbinding tussen de bron en het waarneempunt,
bestaande uit rechtlijnige segmenten en die deze snijvlakken omvat, de verticale randen
die in aanmerking worden genomen bij de constructie van het lateraal gebogen voortplantingspad.
Om de demping door het grondeffect voor een lateraal gebogen voortplantingspad te
berekenen, wordt het gemiddelde grondvlak tussen de bron en het waarneempunt berekend,
rekening houdend met het grondprofiel dat verticaal onder het voortplantingspad ligt.
Als in de projectie op een horizontaal vlak een lateraal voortplantingspad de projectie
van een gebouw doorsnijdt, wordt dit in aanmerking genomen in de berekening van Gpath(meestal met G = 0) en in de berekening van het gemiddelde grondvlak met de verticale hoogte van het
gebouw.
Reflecties op verticale obstakels
Demping door absorptie
De reflecties op verticale obstakels worden door middel van spiegelbronnen behandeld.
Reflecties op gevels van gebouwen en geluidweringen worden dus op deze wijze behandeld.
Oppervlakken van objecten worden alleen als reflecterend beschouwd als ze minder dan
15° aflopen in verhouding tot de verticaal. Reflecties worden alleen in aanmerking
genomen voor paden in het verticale voortplantingsvlak, dus niet voor lateraal gebogen
paden. Voor de invallende en gereflecteerde paden, en in de veronderstelling dat het
reflecterend oppervlak verticaal is, wordt het punt van reflectie (dat op het reflecterende
object ligt) geconstrueerd met behulp van rechte lijnen onder homogene, en gebogen
lijnen onder gunstige voortplantingscondities. De hoogte van het reflecterende object
moet, gemeten door het punt van reflectie en gezien vanuit de richting van de invallende
straal, ten minste 0,5 m bedragen. Na projectie op een horizontaal vlak moet de breedte
van het reflecterend object, gemeten door het punt van reflectie en gezien vanuit
de richting van de invallende straal, ten minste 0,5 m bedragen.
NB: reflecties op de grond worden hier niet behandeld. Deze worden bij de berekeningen
van demping door de grens (grond, diffractie) in aanmerking genomen.
Als LWS het vermogensniveau van de bron S is, en αr de absorptiecoëfficiënt van het oppervlak van het obstakel is zoals gedefinieerd
door EN1793-1:2013, dan is het vermogensniveau van de spiegelbron S’ gelijk aan:
|
LWS' = LWS + 10 ∙ lg(1-αr) = LWS + Arefl
|
(2.5.34)
|
waarbij 0 ≤ αr < 1
De hierboven beschreven voortplantingsdempingen worden dan op dit pad (spiegelbron,
waarneempunt) als voor een rechtstreeks pad toegepast.
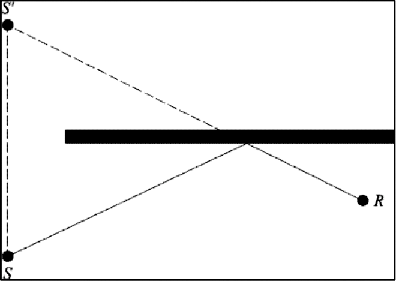
Figuur 2.5.g, Spiegelende reflecties op een obstakel behandeld volgens de spiegelbronmethode
(S: bron, S′: spiegelbron, R: waarneempunt)
Demping door retro-diffractie
In het geometrische onderzoek van geluidspaden hangt het aandeel van de energie dat
door een verticaal obstakel (muur, gebouw) wordt gereflecteerd af van de afstand van
het punt waar de straal aankomt tot de bovenste rand van het obstakel. Dit verlies
van akoestische energie wanneer de straal wordt gereflecteerd, wordt demping door
retro-diffractie genoemd.
In het geval van mogelijk meerdere reflecties tussen twee verticale wanden wordt ten
minste de eerste reflectie in aanmerking genomen.
Bij een open tunnelbak (zie bijvoorbeeld figuur 2.5.h) wordt de demping door retro-diffractie
toegepast op elke reflectie op de steunmuren.
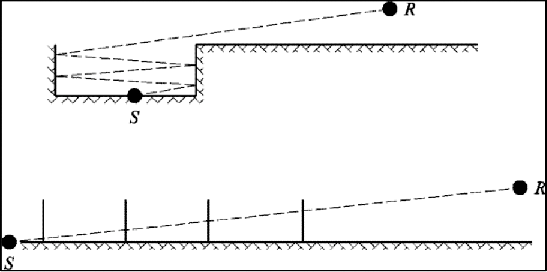
Figuur 2.5.h, Geluidsstraal die vier keer in een baan in een open tunnelbak wordt
gereflecteerd: werkelijk dwarsprofiel (boven), opengevouwen dwarsdoorsnede (onder)
In deze afbeelding bereikt de geluidsstraal het waarneempunt ‘door achtereenvolgens
door de steunmuren van de open tunnelbak te gaan’, die daarom met openingen kunnen
worden vergeleken.
Bij de berekening van voortplanting door een opening is het geluidsveld op het waarneempunt
de som van het directe veld en het door de randen van de opening gediffracteerde veld.
Dit gediffracteerde veld zorgt voor de continuïteit van de overgang tussen het gebied
met direct zicht en het schaduw gebied. Wanneer de straal de rand van de opening nadert,
wordt het directe veld gedempt. De berekening is identiek aan die van de demping door
een geluidsscherm in het vrije gebied.
Het padverschil δ’ in verband met elke retro-diffractie is het tegenovergestelde van het padverschil
tussen S en R relatief op elke bovenrand O, en dit in een weergave volgens een ingezette
dwarsdoorsnede (zie figuur 2.5.i).
|
δ' = – (SO + OR – SR)
|
(2.5.35)
|

Figuur 2.5.i, Het padverschil voor de tweede reflectie
Het ‘min’-teken van vergelijking (2.5.35) betekent dat het waarneempunt hier in het
gebied met direct zicht in aanmerking wordt genomen.
Demping via retro-diffractie ∆retrodif wordt verkregen met behulp van vergelijking (2.5.36), die lijkt op vergelijking (2.5.21)
met bewerkte notaties.
Deze demping wordt toegepast op de rechtstreekse straal telkens wanneer die ‘door’
een muur of gebouw gaat (reflecteert). Het vermogensniveau van de spiegelbron S’ wordt
dus:
|
LW' = LW + 10lg(1 – αr) – ∆retrodif
|
(2.5.37)
|
In complexe voortplantingsconfiguraties kunnen diffracties tussen reflecties of tussen
het waarneempunt en de reflecties bestaan. In dit geval wordt de retro-diffractie
door de wanden geschat door het pad tussen de bron en het eerste diffractiepunt R’
(dat derhalve in vergelijking (2.5.35) als het waarneempunt wordt beschouwd) in aanmerking
te nemen. Dit beginsel wordt weergegeven in figuur 2.5.j.
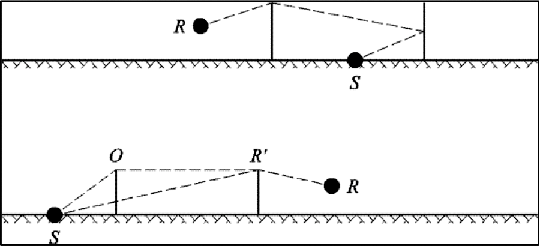
Figuur 2.5.j, Het padverschil in de aanwezigheid van een diffractie: werkelijke dwarsdoorsnede
(boven), opengevouwen dwarsdoorsnede (onder)
In het geval van meerdere reflecties worden de reflecties door elke individuele reflectie
toegevoegd.
Wanneer er een reflecterend geluidscherm of reflecterend obstakel in de buurt van
het spoor is, worden de geluidsstralen van de bron achtereenvolgens gereflecteerd
door dit obstakel en door het zijvlak van het spoorvoertuig. Onder deze omstandigheden
gaan de geluidsstralen tussen het obstakel en de carrosserie van het spoorvoertuig
door voordat ze van de bovenrand van het obstakel worden afgebogen.
Om rekening te houden met meerdere reflecties tussen een spoorwegvoertuig en een nabijgelegen
obstakel, wordt het geluidsvermogen van een enkele equivalente bron berekend. In deze
berekening worden grondeffecten genegeerd.
Voor het afleiden van het geluidsvermogen van de equivalente bron gelden de volgende
definities:
-
• De oorsprong van het coördinatensysteem is de linker railkop
-
• Een echte bron bevindt zich op S (ds=0, hs), waarbij hs de hoogte van de bron ten opzichte van de railkop is
-
• Het vlak h=0 definieert de carrosserie van het voertuig
-
• Een verticaal obstakel met de bovenkant bij B (dB, hb)
-
• Een waarneempunt dat zich bevindt op een afstand dR > 0 achter het obstakel waar R de coördinaten (dB+dR, hR) heeft
De binnenzijde van het obstakel heeft absorptiecoëfficiënten α(f) per octaafband. De carrosserie van het spoorvoertuig heeft een equivalente reflectiecoëfficiënt
Cref. Normaal gesproken is Cref gelijk aan 1. Alleen in het geval van open, platte goederenwagons kan een waarde
van 0 worden gebruikt. Als dB>5hB of α(f) > 0,8 is, wordt er geen rekening gehouden met de interactie van de trein en het scherm.
In deze configuratie kunnen meerdere reflecties tussen de carrosserie van het spoorvoertuig
en het obstakel worden berekend met behulp van spiegelbronnen die zich op Sn(dn = -2n • dB, hn = hs), n=0,1,2,..N bevinden; zoals weergegeven in figuur 2.5.k.
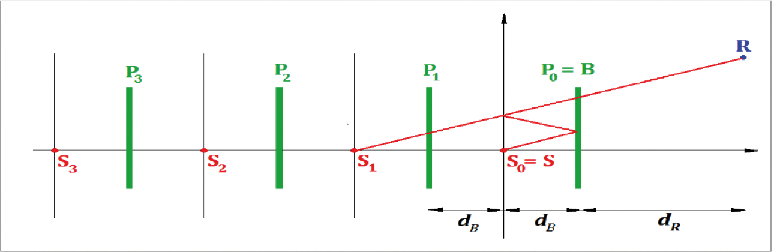
figuur 2.5.k. Weergave van de modellering meervoudige reflecties tussen trein en geluidscherm.
Het geluidsvermogen van de equivalente bron wordt uitgedrukt door:
Waar het geluidsvermogen van de gedeeltelijke bronnen wordt verkregen door:
|
LW,n = LW + ∆Lgeo,n+ ∆Ldif,n + ∆Labs,n + ∆Lref,n + ∆Lretrodif,n
|
(2.5.39)
|
Met:
|
LW
|
het geluidsvermogen van de echte bron
|
|
∆Lgeo,n
|
een correctieterm voor geometrische uitbreiding
|
|
∆Ldif,n
|
een correctieterm voor diffractie door de bovenkant van het obstakel
|
|
∆Labs,n
|
een correctieterm voor de absorptie aan de binnenzijde van het obstakel
|
|
∆Lref,n
|
een correctieterm voor de reflectie van de carrosserie van het spoorvoertuig
|
|
∆Lretrodif,n
|
een correctieterm voor de eindige hoogte van het obstakel als een reflecterend object
|
De correctie voor geometrische uitbreiding wordt verkregen door
De correctie voor diffractie door de bovenkant van het obstakel wordt verkregen door
(2.5.42):
|
∆Ldif,n = D0 – Dn
|
(2.5.42)
|
Waarbij Dn de demping door diffractie is, berekend met formule (2.5.21) waarin C’’ = 1 voor het pad dat de bron Sn verbindt met het waarneempunt R, rekening houdend met diffractie aan de bovenkant
van het obstakel B:
|
δn = ± (| SnB | + | BR | – | SnR |)
|
(2.5.43)
|
De correctie voor absorptie aan de binnenzijde van het obstakel wordt verkregen door:
|
∆Labs,n = 10 ∙ n ∙ lg(1 – α)
|
(2.5.44)
|
De correctie voor de reflectie van de carrosserie van het spoorvoertuig wordt verkregen
door:
|
∆Lref,n= 10 ∙ n ∙ lg ((Cref)
|
(2.5.45)
|
De correctie voor de eindige hoogte van het reflecterend obstakel wordt door middel
van retro-diffractie in aanmerking genomen. Het straalpad dat overeenkomt met een
afbeelding in de orde van N > 0 wordt n maal gereflecteerd door het obstakel. In de
dwarsdoorsnede vinden deze reflecties plaats op de afstanden di= –(2i – q)db, i = 1,2,..n. Met Pi (d = di, h = hb), i = 1,2,..n als de bovenkant van deze reflecterende oppervlakken. Op elk van deze punten wordt
een correctieterm berekend als:
Waarbij ∆Lretrodif,n,i wordt berekend voor een bron op positie Sn, de bovenkant van een obstakel op Pi en een waarneempunt op positie R'. De positie van het equivalente waarneempunt R' wordt verkregen door R'=R als het waarneempunt zich boven de zichtlijn van Sn van naar B bevindt; anders wordt de positie van het equivalente waarneempunt ingenomen op de
zichtlijn verticaal boven het echte waarneempunt; dat zijn
