Normering met een vaardigheidsschaal bij de centrale examens Nederlandse taal en rekenen
in het mbo en de rekentoets vo (rvo)
Doel van normering met een vaardigheidsschaal
Zoals gebruikelijk bij toetsen en examens, worden bij de rekentoetsen VO en de centrale
examens Nederlandse taal en rekenen in het MBO cijfers toegekend. De manier waarop
deze cijfers bepaald worden, noemen we ‘normering met een vaardigheidsschaal’.
Het gebruik van een vaardigheidsschaal is vooral geschikt als er meerdere varianten
van een examen zijn. De ene variant kan net iets makkelijkere opgaven hebben dan de
andere variant. Dit kan gebeuren omdat de moeilijkheid van een opgave niet heel precies
ingeschat kan worden voordat deze is voorgelegd aan examenkandidaten. Bij het toekennen
van cijfers moet daar rekening mee gehouden worden. Op de makkelijkere varianten moet
een kandidaat dan iets meer vragen goed beantwoord hebben om een 6 te krijgen. We
kunnen ook zeggen: een kandidaat moet eenzelfde vaardigheid aantonen voor een 6, ongeacht
de variant die hij maakt, ongeacht het jaar waarin het examen wordt afgelegd dan wel
de examenperiode binnen dat jaar. En dit moet ook gelden voor ieder ander cijfer.
Ongeacht de variant die gemaakt wordt, moet eenzelfde aangetoonde vaardigheid steeds
beloond worden met eenzelfde cijfer.
Meten van vaardigheid
Het cijfer dat toegekend wordt, wordt dus bepaald door de vaardigheid die een kandidaat
heeft. Deze vaardigheid kan hij aantonen door opgaven van een examen goed te maken.
Het examen is daarmee een meetinstrument geworden van de vaardigheid van de kandidaat.
En net zoals een thermometer een meetinstrument is van de temperatuur, op de Celsius-
of Fahrenheit-schaal, zo spreken we ook van een vaardigheidsschaal.
De lengte van mensen meten we normaal gesproken met een meetlat. Stel dat die niet
uitgevonden was, dan zouden we de hoogte van muurtjes kunnen gebruiken om de lengte
van mensen te meten: wie erover heen kijkt, is langer dan degene die dat niet kan.
Op analoge wijze kunnen we opgaven gebruiken om de vaardigheid van kandidaten te meten:
wie de opgave goed maakt, is vaardiger dan degene die dat niet kan. In Figuur 1 is
een vaardigheidsschaal afgebeeld. De vaardigheden van de kandidaten en de moeilijkheden
van de opgaven zijn streepjes op eenzelfde meetlat ofwel schaal. Kandidaten met een
hoge vaardigheid hebben een grotere kans om opgaven goed te maken dan kandidaten met
een lagere vaardigheid. Omgekeerd, opgaven met een hoge moeilijkheid worden minder
vaak goed gemaakt dan opgaven met een lage moeilijkheid.
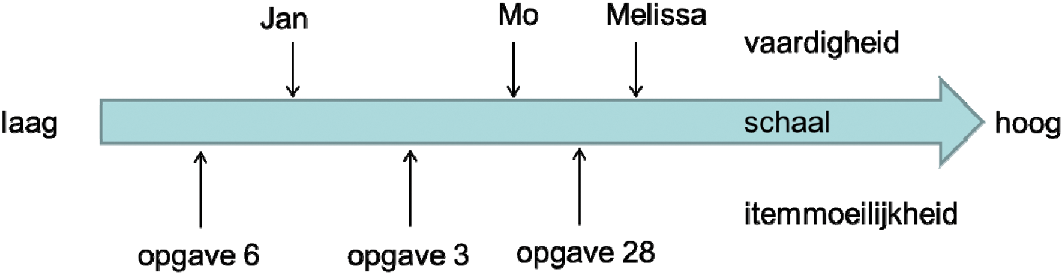
Figuur 1. Afbeelding van personen en opgaven op één vaardigheidsschaal
Een opgave heeft altijd dezelfde moeilijkheid; een examenvariant kan bestaan uit makkelijkere
of moeilijkere opgaven. Een mini-examenvariant met alleen opgave 6 en opgave 3 uit
bovenstaand voorbeeld, is bijvoorbeeld gemakkelijker dan een mini-examenvariant met
alleen opgave 3 en opgave 28. Uit het antwoordgedrag van voldoende leerlingen op de
makkelijke variant, kunnen we afleiden hoeveel makkelijker opgave 6 is dan opgave
3. Uit het antwoordgedrag van andere leerlingen op de moeilijke variant, kunnen we
afleiden hoeveel moeilijker opgave 28 is dan opgave 3. Door een koppeling van deze
twee verschillen, kunnen we afleiden hoeveel moeilijker opgave 28 is dan opgave 6.
Op deze manier kunnen de moeilijkheden van alle opgaven op dezelfde schaal worden
afgebeeld. Meer details over de schatting van itemmoeilijkheden staan in de sectie
Schattingsmethode.
Getallen bij de vaardigheidsschaal
De schattingen van punten op de vaardigheidsschaal liggen vast op een lineaire transformatie
na. We mogen bij alle punten dus een willekeurig aantal optellen, of alle punten met
een willekeurige constante vermenigvuldigen. Een vaardigheidsschaal wordt geschat
om scores op verschillende examenvarianten met elkaar te vergelijken. De precieze
getallen die eraan hangen, zijn in wezen keuzes. Het nulpunt komt vrij willekeurig
ergens te liggen. Negatieve vaardigheidsscores zijn lager dan vaardigheidsscore 0.
Dit heeft geen inhoudelijke betekenis. We hadden bij alle scores ook 100 punten op
kunnen tellen. In technische termen: de vaardigheidsschaal is van interval-niveau.
Vergelijk met een temperatuur-schaal: het nulpunt op de Fahrenheit-schaal ligt ergens
anders dan op de Celsius-schaal, maar voor beide geldt: hoe hoger, hoe warmer.
Je kunt bij temperatuur niet spreken van ‘het is vandaag twee keer zo warm als gisteren’,
want voor zo’n uitspraak is een absoluut nulpunt nodig. Dat is er op de Fahrenheit-
en Celsiusschaal niet. Zo kun je dus ook niet zeggen dat een kandidaat twee keer zo
vaardig is als een andere kandidaat. Er is wel een inhoudelijke betekenis van negatieve
graden op de Celsius-schaal (het vriest), maar op de Fahrenheit-schaal vriest het
al onder 32 graden en is deze inhoudelijke betekenis van negatieve temperaturen er
dus niet. Zo’n inhoudelijke betekenis van het nulpunt is er bij de vaardigheidsschaal
ook niet.
Om nog technischer te worden: de ratio van twee verschillen is bij een interval-schaal
wel interpreteerbaar. Dus als Jan, Mo, Mieke en Melissa respectievelijk 80, 90, 100
en 120 als vaardigheidsscores hebben, dan kun je wel zeggen dat het verschil in vaardigheid
tussen de meisjes Mieke en Melissa (20 punten) twee keer zo groot is als het verschil
tussen de jongens Jan en Mo (10 punten).
Van score naar vaardigheid
Als de moeilijkheden van alle opgaven of items in een examenperiode geschat zijn,
wordt een beste schatting van de vaardigheid van een kandidaat gemaakt1 aan de hand van de items die de kandidaat daadwerkelijk zijn voorgelegd. Van alle
antwoorden die een kandidaat geeft, wordt eerst de ruwe score berekend, ofwel het
aantal behaalde punten. In combinatie met de itemkenmerken waarop deze ruwe score
behaald is, wordt de vaardigheid geschat. Dit gebeurt per examenvariant voor iedere
ruwe score apart, zie bijvoorbeeld tabel 1 voor een gedeelte van de omzettingstabel
van score naar vaardigheid bij variant 2 van een toets of examen. De relatie tussen
score en vaardigheid hoeft niet rechtlijnig te zijn. Dit hangt af van de onderlinge
verschillen in moeilijkheid tussen de opgaven.
Tabel 1. Voorbeeld van een omzettingstabel score naar vaardigheid
|
Variant
|
Score
|
Vaardigheid
|
|
...
|
...
|
|
|
V2
|
30
|
66.5
|
|
V2
|
31
|
70.0
|
|
V2
|
32
|
73.7
|
|
V2
|
33
|
77.8
|
|
V2
|
34
|
82.3
|
|
V2
|
35
|
87.3
|
|
V2
|
36
|
93.0
|
|
...
|
...
|
|
Deze methode levert dus per examenvariant een tabel op met achter iedere mogelijke
ruwe score een vaardigheidsschatting. De ruwe score loopt van 0 tot en met de maximale
score. De vaardigheidsschatting heeft niet overal dezelfde nauwkeurigheid. Bij de
allerlaagste en allerhoogste scores is de meetnauwkeurigheid lager dan ergens in het
midden van de scores. De exacte score waarbij de meetnauwkeurigheid het hoogst is,
hangt af van de moeilijkheid van de opgaven in de examenvariant.
Als er opgaven in een examenvariant zitten, waarover de normeringsvergadering beslist
dat zij niet mee mogen tellen bij de beoordeling van een kandidaat, dan noemen we
dit geneutraliseerde items. Alle kandidaten krijgen voor een geneutraliseerd item
het maximale aantal punten dat behaald kan worden. Bij de schatting van de itemparameters
doen de geneutraliseerde items niet mee, alleen de antwoorden op de overige items
worden gebruikt voor het vaststellen van de vaardigheidsschaal. Bij de schatting worden
de geneutraliseerde items buiten beschouwing gelaten.
De vaardigheid van de kandidaat wordt dus eigenlijk geschat aan de hand van de antwoorden
op een verkorte examenvariant, waarin de geneutraliseerde items niet opgenomen zijn.
In tabel 2 staat een voorbeeld van de omzettingstabel van score naar vaardigheid als
er in een variant, waarop maximaal 54 punten behaald kunnen worden, drie geneutraliseerde
items van ieder maximaal 1 punt zijn. De schatting van de vaardigheid gaat uitsluitend
over de verkorte variant, met scores 0 tot en met 51. De rapportage gaat over de gehele
range 0 tot en met 54. De ‘neutrale punten’ worden bij de verkorte score opgeteld
om tot de score op de volledige variant te komen. In de rapportage-tabel staat achter
de scores 0, 1 en 2 dezelfde vaardigheid als bij de laagst mogelijke score 3, namelijk
vaardigheid 75. Echter, in praktijk komen deze scores niet voor omdat iedere kandidaat
minimaal 3 punten scoort, namelijk op de geneutraliseerde items.
Tabel 2. Vaardigheidsscores bij een examenvariant met 3 geneutraliseerde items van
ieder 1 punt
|
Schatting
|
Rapportage
|
|
Score verkorte variant
|
Vaardigheid
|
Score volledige variant
|
Vaardigheid
|
|
Nvt
|
nvt
|
0
|
75
|
|
Nvt
|
nvt
|
1
|
75
|
|
Nvt
|
nvt
|
2
|
75
|
|
0
|
75
|
3
|
75
|
|
1
|
83
|
4
|
83
|
|
2
|
86
|
5
|
86
|
|
..
|
|
..
|
|
|
51
|
212
|
54
|
212
|
Noot. Gerapporteerde scores 0,1 en 2 komen niet voor, vanwege de geneutraliseerde items.
Van vaardigheid naar cijfer
Door middel van item respons theorie-schaling worden alle kandidaten en opgaven op
dezelfde vaardigheidsschaal afgebeeld. Cijfers reflecteren de waardering voor behaalde
vaardigheid. Het belangrijkste punt op de vaardigheidsschaal is de cesuur: vanaf de
cesuur-vaardigheid wordt de vaardigheid van kandidaten als voldoende beoordeeld. Een
vaardigheid onder de cesuur wordt als onvoldoende beoordeeld.
Om afrondingsproblemen te voorkomen, is het precieze cijfer dat wordt toegekend bij
de cesuur-vaardigheid afhankelijk van het aantal gerapporteerde decimalen. Als hele
cijfers gerapporteerd worden, zoals bij de Rekentoets vo of het centraal examen Rekenen,
is het cijfer bij de cesuur een 5,5. Als cijfers met één decimaal worden gerapporteerd,
zoals bij het centraal examen Taal, is het cijfer bij de cesuur gelijk aan 5,45. In
Figuur 2 is dit bij vaardigheid 83,0.
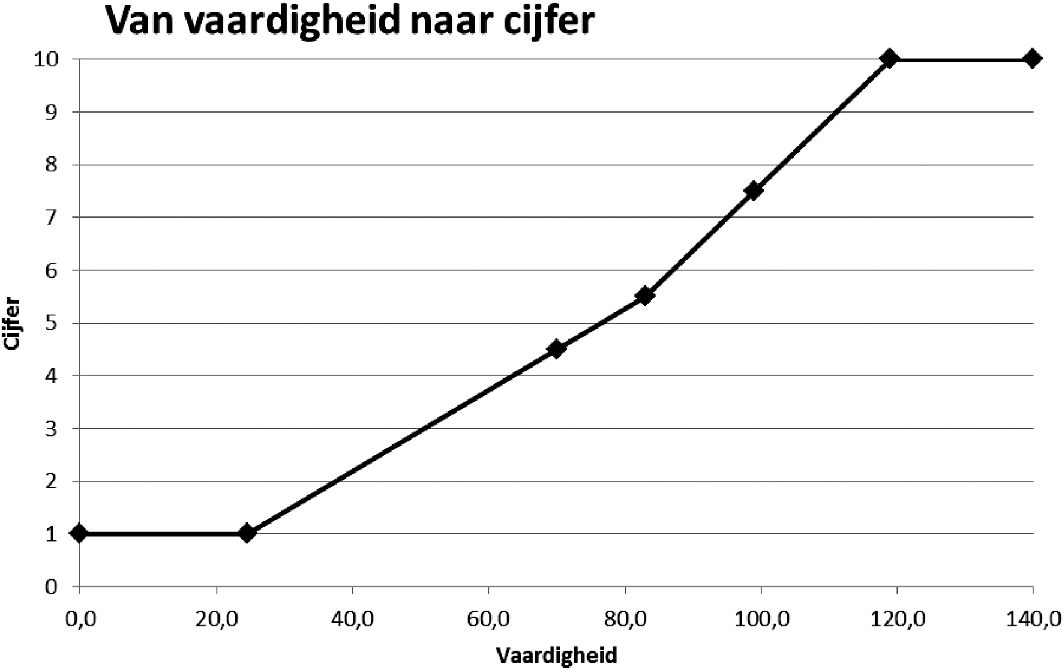
Figuur 2. Voorbeeld van omzetting van vaardigheidsscores naar cijfers
De omzetting van vaardigheid naar cijfer is lineair met een knik. Dat wil zeggen dat
er een rechtlijnig verband is tussen cijfer en vaardigheid boven de cesuur, en dat
er een ander rechtlijnig verband is onder de cesuur. Om de relaties exact vast te
leggen, worden door de normeringsvergadering nog twee cijferpunten op de vaardigheidsschaal
vastgelegd: één boven de cesuur en één onder de cesuur. Boven de cesuur is dit punt
het cijfer 7,5, waarmee het cijfer 8 of hoger wordt toegekend aan kandidaten met een
goede vaardigheid. Onder de cesuur wordt het cijfer 4,5 of 3,5 vastgesteld.
De drie punten op de vaardigheidsschaal die de omzetting van vaardigheid naar cijfer
bepalen, noemen we ook wel standaarden. De rechte lijnen die door de drie punten bepaald
worden, worden naar boven en beneden afgekapt. Cijfer boven 10,0 en onder 1,0 worden
immers niet toegekend. Het bepalen van de waarden van standaarden wordt Standaardsetting
genoemd. Meestal worden daarvoor de oordelen van experts gebruikt. Er zijn diverse
methodes waarbij deze experts oordelen per opgave moeten geven, of waarbij zij oordelen
over sets van opgaven moeten geven.
Schattingsmethode
Om de moeilijkheid van de opgaven precies te schatten, wordt gebruik gemaakt van item
respons theorie (IRT). Opgaven worden binnen deze theorie items genoemd. De antwoorden
van leerlingen worden responsen genoemd. De kans dat een bepaalde kandidaat een bepaald
item goed beantwoordt, is afhankelijk van de vaardigheid van de persoon en van kenmerken
van het item, zoals de moeilijkheid ervan. De vaardigheid van een kandidaat wordt
met de Griekse letter θ aangeduid. De kans dat een kandidaat met een vaardigheid θ
een item goed maakt, wordt omschreven met een wiskundige formule of functie. Van de
familie van modellen die binnen de IRT vallen, wordt in dit geval het one parameter
logistic model (OPLM, Glas & Verhelst, 1989, Verhelst & Glas, 1993; Verhelst, Glas
& Verstralen, 1993; Verhelst & Eggen, 2011) gebruikt. De itemresponsfunctie van het
OPLM is gegeven door
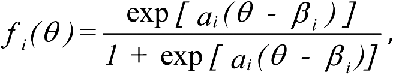
waarin ai de zogenaamde discriminatie-index van het item is, en βi de moeilijkheidsparameter van item i is. In Figuur 3 zijn de itemresponscurven weergegeven van twee items i en j, die even moeilijk zijn maar verschillend discrimineren. Als de vaardigheid van de
kandidaat gelijk is aan de moeilijkheid van een opgave, dan heeft hij een kans van
50% om de opgave goed te maken. Opgaven met een hoge discriminatie-index onderscheiden
beter tussen hoog- en laagvaardige kandidaten, ofwel de kans om een opgave goed te
maken, neemt hierbij snel toe met θ. De index ai wordt ook wel de hellingsparameter genoemd.
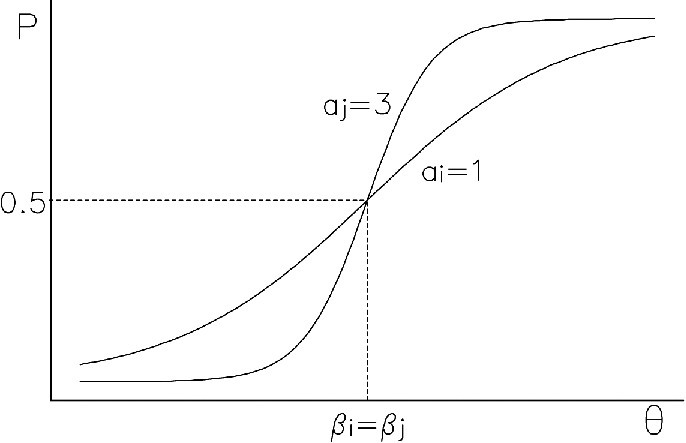
Figuur 3. Twee itemresponscurven in het OPLM: zelfde moeilijkheid, verschillende discriminatie-index
Een vaak toegepaste schattingsmethode voor de moeilijkheidsparameters βi is de ‘conditionele grootste aannemelijkheidsmethode’ (in het Engels: Conditional
Maximum Likelihood, verder aangeduid als CML). Die maakt gebruik van het feit dat
in het model een afdoende steekproefgrootheid ('sufficient statistic') bestaat voor
de latente variabele θ, namelijk de ruwe score of het aantal correct beantwoorde items.
Dat betekent grofweg dat, indien de itemparameters bekend zijn, alle informatie die
het antwoordpatroon over de vaardigheid bevat, kan worden samengevat in de ruwe score;
het doet er dan verder niet meer toe welke opgaven goed en welke fout zijn gemaakt.
Hieruit vloeit voort dat de conditionele kans op een juist antwoord op item i, gegeven de ruwe score, een functie is die alleen afhankelijk is van de itemparameters
en onafhankelijk van de waarde van θ2. De CML-schattingsmethode maakt van deze functie gebruik. Deze methode maakt geen
enkele vooronderstelling over de verdeling van de vaardigheid in de populatie, en
is ook onafhankelijk van de wijze waarop de steekproef is getrokken. Door de indices
ai te beperken tot (positieve) gehele getallen, en door ze a priori als constanten in
te voeren, is het mogelijk CML-schattingen van de itemparameters βi te maken.
Standaardsetting
Bij een standaardsetting wordt een punt op de vaardigheidsschaal bepaald (figuur 4).
Uitgangspunt voor de standaardbepaling was de gehanteerde procedure en de bijbehorende
uitkomsten van het standaardsettingsonderzoek bij de referentiesets. Bij de referentiesets
is gebruik gemaakt van standaardsetting-procedures met beoordelaars, in casu de Angoff-procedure en de Bookmark-procedure. Merk op dat deze methoden niet beperkt hoeven te zijn tot de cesuur voor een voldoende,
maar ook toegepast kunnen worden voor het cijfer 5 of 8.
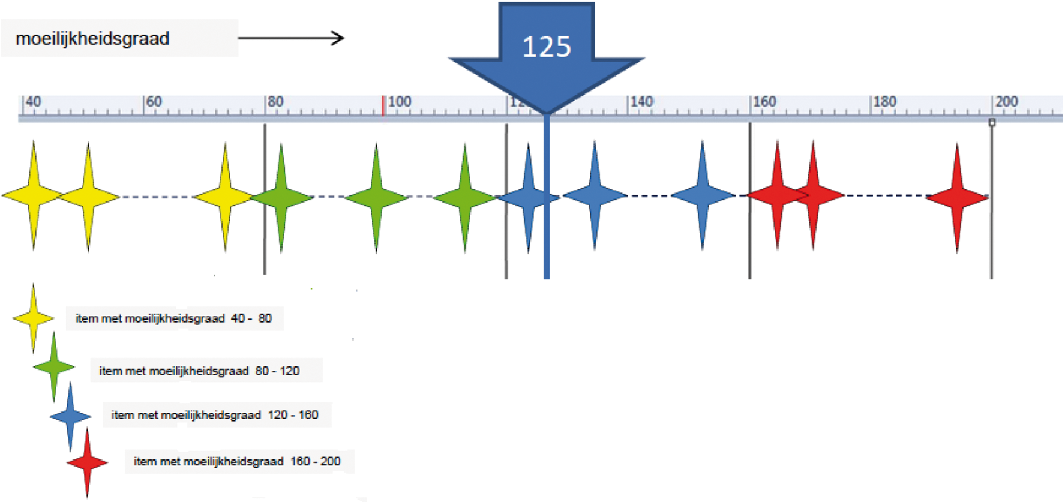
Figuur 4. Standaard (125) op een vaardigheidsschaal
Angoff-procedure
Bij een Angoff-procedure moeten de experts een grenskandidaat in gedachten nemen.
Een grenskandidaat is een kandidaat die het vereiste niveau net beheerst. De experts
geven per item aan of een grenskandidaat deze goed maakt of niet. Bij een gemodificeerde
Angoff-procedure wordt per item door de experts de kans ingeschat dat een grenskandidaat
de opgave goed maakt. Dit is hetzelfde als inschatten hoeveel van 100 grenskandidaten
de opgave goed maken. Optellen van de kansen van alle opgaven van een bepaald examen
of toets geeft de grensscore die gehaald moet worden op het betreffende examen of
toets om te voldoen aan minimale eisen: de cesuur. Deze cesuur wordt vervolgens afgebeeld
op de vaardigheidsschaal, waarmee de standaard bepaald is.
Bookmark-procedure
Als er ook afnamegegevens beschikbaar zijn, kan ook gewerkt worden met een Bookmark-procedure,
waarbij gebruik gemaakt wordt van de empirische ordening van de items naar moeilijkheid
(Van der Schoot, 2001, 2008). Deze procedure voor het vaststellen van een standaard
voor een bepaald niveau maakt gebruik van een reeks opgaven die naar moeilijkheid
zijn gerangschikt. Deskundigen geven aan welke opgave nog wel en welke niet meer beheerst
zouden moeten worden door een grenskandidaat. In de reeks opgaven plaatsen zij een
‘bookmark’. Experts geven dus aan hoeveel items van een set opgaven beheerst moeten
worden op een bepaald niveau. Dit oordeel wordt weer omgezet in een punt op de vaardigheidsschaal.
Hieronder wordt voor rekenen en Nederlandse taal beschreven hoe de standaardsettingsprocedure
is verlopen.
Procedure rekenen
Gedurende de standaardbepalingsprocedure van de referentiesets rekenen is gebruik
gemaakt van de Extended Angoff methode. Voor deze procedure zijn de panelleden in
drie groepen verdeeld. Bij de groepsindeling is rekening gehouden met de achtergrond
van panelleden. Elke groep heeft een gedeelte van het materiaal beoordeeld. Na een
individuele beoordelingsronde (ronde 1) hebben de panelleden in kleine groepen de
opgaven besproken. Tijdens deze discussieronde was het mogelijk om het oordeel dat
in de individuele ronde gegeven was aan te passen (ronde 2). De discussieronde is
zodanig georganiseerd dat de opgaven in kleine groepen van wisselende samenstelling
zijn besproken. Aangezien slechts een gedeelte van de opgaven door een panellid beoordeeld
is, is door middel van een omzettingstabel (gebaseerd op een vaardigheidsschaal) de
grensscore op het beoordeelde gedeelte geëxtrapoleerd naar de volledige referentieset.
Naast de Extended Angoff procedure is ook een Bookmarkprocedure uitgevoerd. Voor deze
procedure is op basis van de verzamelde data de moeilijkheid van opgaven bepaald3. De opgaven zijn vervolgens geordend van makkelijk naar moeilijk. Panelleden konden
aangeven tot en met welke opgave een grenskandidaat een kans van 67% of minder had
om de opgave goed te maken.
De uitkomsten van beide procedures zijn in een plenaire discussie voorgelegd aan de
panelleden. Hierbij werd weergegeven wat het percentage leerlingen zou zijn dat het
referentieniveau zou halen. Daarnaast is deze voorlopige cesuur vergeleken met reeds
vastgestelde cesuren, namelijk de tot nu toe gehanteerde rekenen 2F en 3F standaarden
voor de centrale examens en de Rekentoets vo. Vervolgens hebben alle experts op schrift
een definitief oordeel gegeven. Het gemiddelde van deze oordelen geldt vervolgens
als uiteindelijk advies aan het College voor Toetsen en Examens.
Procedure Nederlandse taal
Gedurende de standaardbepalingsprocedure is gebruik gemaakt van de Extended Angoff
methode. Voor deze procedure zijn de panelleden in vier groepen verdeeld. Elke groep
heeft een gedeelte van het materiaal beoordeeld. Na een individuele beoordelingsronde
(ronde 1) hebben de panelleden in kleine groepen de opgaven besproken. Tijdens deze
discussieronde was het mogelijk om het oordeel dat in de individuele ronde gegeven
was aan te passen (ronde 2).
Na afloop van deze discussieronde konden experts hun oordelen intekenen in een figuur.
In deze figuur werden de opgaven die een expert beoordeeld had afgebeeld op de volledige
schaal van de referentieset. Door zorgvuldig de oordelen uit de inhoudelijke rondes
in de figuur in te tekenen kon het oordeel op een gedeelte van de opgaven daarmee
geëxtrapoleerd worden naar de volledige referentieset. Zo konden experts tot een eerste
advies over de cesuur op de volledige referentieset komen.
Naar aanleiding van dit eerste advies is nagegaan wat de gemiddelde cesuur van alle
panelleden op de referentieset zou zijn. Voor deze cesuur is bekeken wat het percentage
kandidaten zou zijn dat het referentieniveau zou halen. Daarnaast is deze voorlopige
cesuur vergeleken met reeds vastgestelde cesuren, namelijk de CENTRALE EXAMENS Taal
2F en 3F-cesuur. Vervolgens hebben alle experts op schrift een definitief oordeel
gegeven. Het gemiddelde van deze oordelen geldt vervolgens als uiteindelijk advies
aan het College voor Toetsen en Examens. Het College heeft de adviezen overgenomen
en vastgesteld.
Omzetting referentiecesuur naar cesuur centraal examen taal en rekenen en rekentoets
vo-cesuur
Door de items uit de referentieset rekenen en die uit de varianten van de centrale
examens rekenen en de rekentoets vo af te beelden op dezelfde vaardigheidsschaal (zie
figuur 1 en de beschrijving in paragraaf 4) wordt de referentiecesuur (= de cesuur
van de referentieset) overgebracht op iedere variant van het centraal examen rekenen
en de rekentoets vo. Geheel analoog wordt de referentiecesuur Nederlandse taal op
de varianten van de centrale examens Nederlandse taal overgebracht.
Omzetting van scores in cijfers
Van iedere toets- en examenvariant wordt de omzetting van scores in cijfers bepaald
door de scores om te zetten in vaardigheidsniveaus op de wijze waarop dat in paragraaf
4 is beschreven en door de vaardigheidsniveaus om te zetten in cijfers volgens paragraaf
5. De omzetting van scores verloopt daardoor via een vaardigheidsschaal.
Tabel 3a is een voorbeeld van een omzettingstabel van scores – via vaardigheidsniveaus
– in cijfers.
Mogelijkheid van maatwerk bij de normering
Het is mogelijk om bij de normering met een andere cesuur dan de referentiecesuur
te werken. In 2013 is dit voor het eerst gebeurd bij de normering van de rekentoets
2F. Toen is de cesuur voor de kandidaten in de gemengde en theoretische leerweg één
cijferpunt hoger gelegd dan de referentiecesuur, terwijl de cesuur voor de kandidaten
in de basisberoepsgerichte leerweg één cijferpunt lager lag. Tabel 3b respectievelijk
3c is een voorbeeld van een omzettingstabel waarbij de cesuur één cijferpunt lager
respectievelijk hoger ligt dan bij de omzetting van scores in cijfers volgens tabel
3a.
Cijferdifferentiatie (aangepaste normering) bij Nederlandse taal 2F voor entree-en
mbo-2opleidingen
Vanaf 2015–2016 zal voor de studenten uit de entree-opleidingen en de mbo-2 opleidingen
een aangepaste normering gelden. Deze normering ligt op hetzelfde niveau als de normering
Nederlandse taal voor de bb-leerlingen in het vmbo. Dit betekent dat de cesuur en
de bijbehorende cijferverdeling over de tienpuntsschaal met 1 cijferpunt worden verlaagd
ten opzichte van het referentieniveau 2F. Tabel 4 is een voorbeeld van een omzettingstabel
waarbij in kolom 2 de score-cijferverdeling conform de referentiecesuur is toegepast
en in kolom 3 cijferdifferentiatie is toegepast met één cijferpunt lager dan de referentiecesuur.
De reden dat deze cijferdifferentiatie wordt toegepast op beide beroepsopleidingen
is dat eenzelfde differentiatie wordt toegepast op de vooropleiding voor mbo-2, te
weten de basisberoepsgerichte leerweg in het vmbo. Een onverkorte toepassing van de
normering zoals voor de andere leerwegen in het vmbo en mbo-3 zou ertoe leiden dat
onevenredig veel studenten zouden zakken, omdat het vereiste referentieniveau 2F feitelijk
te moeilijk is voor hen. Naar verwachting zou dan een te groot deel zonder diploma
het onderwijs verlaten, hetgeen onwenselijk is.
Tabel 4 Voorbeeld van een fictieve omzettingstabel van een 2F-examen Nederlandse taal
met gebruikmaking van de referentiecesuur en de cijferdifferentiatie voor mbo-2 &
entree
|
Score
|
Schaalscore
|
Cijfer referentiecesuur 2F
|
Cijfer bij cijferdifferentiatie entree en mbo-2
|
|
0
|
0
|
1
|
1
|
|
1
|
0
|
1
|
1
|
|
2
|
0
|
1
|
1
|
|
3
|
1
|
1
|
1
|
|
4
|
2
|
1
|
1
|
|
5
|
3
|
1
|
1
|
|
6
|
4
|
1
|
1
|
|
7
|
6
|
1
|
1
|
|
8
|
7
|
1
|
1
|
|
9
|
9
|
1
|
1
|
|
10
|
10
|
1
|
1
|
|
11
|
12
|
1
|
1
|
|
12
|
14
|
1
|
1,1
|
|
13
|
16
|
1
|
1,5
|
|
14
|
18
|
1
|
1,9
|
|
15
|
20
|
1,1
|
2,1
|
|
16
|
22
|
1,4
|
2,4
|
|
17
|
24
|
1,7
|
2,7
|
|
18
|
26
|
2,0
|
3,0
|
|
19
|
28
|
2,3
|
3,3
|
|
20
|
31
|
2,6
|
3,6
|
|
21
|
33
|
2,9
|
3,9
|
|
22
|
35
|
3,1
|
4,1
|
|
23
|
37
|
3,4
|
4,4
|
|
24
|
39
|
3,6
|
4,6
|
|
25
|
41
|
3,9
|
4,9
|
|
26
|
44
|
4,2
|
5,2
|
|
27
|
46
|
4,5
|
5,5
|
|
28
|
48
|
4,7
|
5,7
|
|
29
|
50
|
4,9
|
5,9
|
|
30
|
52
|
5,2
|
6,2
|
|
31
|
54
|
5,5
|
6,5
|
|
32
|
56
|
5,6
|
6,6
|
|
33
|
57
|
5,7
|
6,7
|
|
34
|
59
|
5,8
|
6,8
|
|
35
|
61
|
6,0
|
7,0
|
|
36
|
63
|
6,2
|
7,2
|
|
37
|
65
|
6,4
|
7,4
|
|
38
|
66
|
6,5
|
7,5
|
|
39
|
68
|
6,7
|
7,7
|
|
40
|
69
|
6,8
|
7,8
|
|
41
|
71
|
7,0
|
8,0
|
|
42
|
72
|
7,2
|
8,2
|
|
43
|
74
|
7,5
|
8,5
|
|
44
|
75
|
7,6
|
8,6
|
|
45
|
77
|
8,0
|
9,0
|
|
46
|
78
|
8,2
|
9,2
|
|
47
|
79
|
8,5
|
9,5
|
|
48
|
80
|
8,8
|
9,8
|
|
49
|
82
|
9,7
|
10
|
|
50
|
83
|
10
|
10
|
|
51
|
84
|
10
|
10
|
|
52
|
85
|
10
|
10
|
Literatuur
Eggen, T.J.H.M., & Verhelst, N.D. (2011). Item calibration in incomplete testing designs.
Psicologica: International Journal of Methodology and Experimental Psychology, 32, 107–132.
Glas, C.A.W., & Verhelst, N.D. (1989). Extensions of the partial credit model, Psychometrika, 54, 635–659.
Van der Schoot, F. (2001). Standaarden voor kerndoelen basisonderwijs. De ontwikkeling van standaarden voor kerndoelen
basisonderwijs op basis van resultaten uit peilingsonderzoek. (Proefschrift Universiteit van Amsterdam). Arnhem, Cito.
Van der Schoot, F. (2008). Onderwijs op peil? Een samenvattend overzicht van 20 jaar PPON. Arnhem, Cito.
Verhelst, N.D., & Engelen, R.J.H. (1999). An ability estimator in the two parameter logistic model based on raw scores. Research memorandum. Arnhem: Cito.
Verhelst, N.D., & Glas, C.A.W. (1993). A dynamic generalization of the Rasch model.
Psychometrika, 58, 395–415.
Verhelst, N.D., Glas, C.A.W., & Verstralen, H.H.F.M. (1993). OPLM: One parameter logistic
model. Computer program and manual. Arnhem: Cito.
Warm, T.A. (1989). Weighted likelihood estimation of ability in item response theory.
Psychometrika, 54, 427–450.
